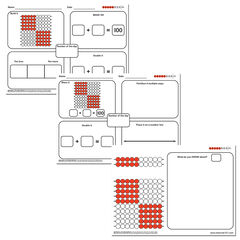
What is Maths Mastery?
Teaching for Maths Mastery is delving deeper into all areas of maths. Rushing through content can risk children only gaining a surface level understanding of concepts. A mastery approach, however, provides opportunities for children to explore mathematical concepts in greater detail, rather than simply memorising procedures or rote learning. Delving deeper enable children to embed and retain their learning, thus developing a secure and adaptable understanding.
The Key Principles are:
- All children can succeed; no one should be left behind
- Whole-class teaching and the use of high-quality text books
- Procedural fluency – e.g. counting, times tables etc.
- More time is taken on each of the key concepts so that the learning is deeper and sustainable
- CPA approach Learning is embedded by the use of Concrete resources – well-thought out Pictorial representations – leading to the ability to think in the Abstract
Who is Maths Mastery for?
Maths mastery is for every child. It is not just for the children who are considered to be the maths ‘masters’ in the classroom, the high achievers. It is for all children to ‘master’ maths. So all children can develop a solid understanding and have the skills to solve a range of mathematical problems.
What are the Benefits of Teaching Maths Mastery?
- Develops children’s self-confidence and resilience.
- Provides more opportunities for children to learn from their mistakes.
- Allows for mistakes to be seen as part of the learning process.
- Reduces the need to reteach concepts, as pupils retain more.
- More time for in-depth exploration of mathematical ideas.
- Enables teachers to distinguish between true conceptual understanding and the memorisation of methods for a short period of time.
- All children exploring mathematical concepts in depth can potentially narrow the attainment gap.
- Lower attaining children can consolidate their understanding.
- Higher attaining children can delve deeper into topics, rather than rushing to new concepts that others might miss.
How do I Teach Maths Mastery?
Taking a mastery approach to teaching mathematics is firstly having the belief that all children can achieve. Secondly, it is providing opportunities for children to delve deeper in all maths subject areas.
The NCETM (National Centre for the Excellence of Teaching in Mathematics) have identified five big ideas in the teaching of maths mastery. These are as follows:
- Coherence – teaching mathematics in a logical sequence, using a small step approach, that builds on prior knowledge and accounts for the skills and knowledge needed for future learning.
- Representation and Structure – visually teaching maths so children can see what a concept looks like.
- Mathematical Thinking – reasoning, problem-solving and making connections.
- Fluency – accurately recalling key number facts, making connections and choosing the correct methods and strategies to solve problems.
- Variation – taking a small step approach to considering what a concept is and what it is not through presenting a concept in different ways.
The Power of Using Manipulatives to Teach Maths Mastery

The Education Endowment Foundation (EFF) cites research evidence indicating that manipulatives should be used with all children, regardless of their mathematical ability. Manipulatives offer a hands-on approach to learning and help children to develop mathematical fluency, reasoning and problem-solving. Through using manipulatives, children can solve problems and visually represent concepts in different ways. Additionally, using manipulatives to explore what a concept is and what it is not offers children a hands-on way to develop a deeper understanding.
Exploring Essential Maths Manipulatives for Teaching for Maths Mastery
In the next part of this blog, we will explore some essential maths manipulatives that can be used across all primary age ranges to teach mastery in a variety of mathematical subjects.
Place Value Counters
Place value counters are a tactile and versatile resource that can be used in both Key Stage 1 and 2.
Here are some of the areas where you can use them.
- Representing multi-digit numbers – Use the different coloured counters to construct numbers, allowing children to see the value of each digit in a number. This is particularly clear when done on a place-value chart, giving children a more concrete understanding of the value of each digit in a number.
- Comparing and ordering numbers – Visually compare numbers by placing numbers constructed from the counters next to each other. Children can then explore which numbers are greater than and less than others, as well as ordering numbers.
- Addition and Subtraction – Use counters in place value charts to represent the numbers to add them together, and to physically remove and exchange counters. An effective way to develop a concrete understanding of formal written methods.
- Multiplication and Division – Use counters to create arrays for multiplication and to physically exchange amounts. Create groups with the counters for division and physically show remainders. As with addition and subtraction, using the counters in place value charts helps to develop a concrete understanding of formal written methods.
- Decimals and Fractions – Use in a place value chart, along with other resources, such as pretend money, bead strings and fraction cards to show the value of decimals and fractions, including equivalents.
Two Coloured Counters
Two-coloured counters can be used in both Key Stage 1 and 2. They are a very diverse resource and can be used to represent numbers in a variety of ways.
Here are some of the areas where you can use them:
- Counting – How many red counters are there? How many blue? How many altogether?
- Subitising – How many counters can you see? How did you work it out?
- Comparing Numbers – How many more red counters are there compared to blue counters? Which is greater/smaller? Is there an odd or even amount?
- Number Bonds – If I have 2 counters, how many more counters do I need to make 10? What if I started with 3 counters? And so on.
- Addition and Subtraction – Use to visually represent the numbers in a calculation. Use with ten frames and place value tables to further enhance understanding, and to create bar models.
- Multiplication and Division – Use to visually represent the numbers in a calculation. Create groups with the counters and arrays to aid understanding.
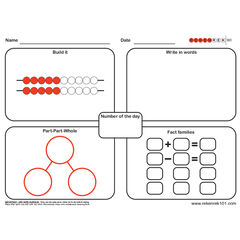
- Part-Whole Relationships (Fractions) – Use the counters to represent fractions, e.g. show 3 red counters and 9 yellow counters. What is the fraction of red/yellow counters? How else can 1/3 be shown using counters etc? Can the children use the counters to show equivalent fractions?
- Ratio – What’s the ratio of yellow counters to red counters?
- Patterns – Use the counters to create regular patterns. What coloured counter comes next?
- Data Collection – Use to create bar graphs with each individual counter representing a given number.
Dienes/Base Ten Sets
Dienes/Base Ten Sets are one of those classroom ‘must haves’. A valuable classroom resource that is very effective at teaching children the value of numbers and what each digit represents.
Here are some of the areas where you can use them:
- Understanding Place Value – Using each cube to represent 1 and using them along side a place value chart is very effective in teaching the value of numbers.
- Represent Number in Different Ways – Use to visually show the value of each digit in numbers with two digits or more. How many tens in 241? What does the 2 represent in the number 241? etc.
- Addition and Subtraction – Children can create the numbers with dienes then physically move the dienes to add them together or exchange for subtraction, providing concrete understanding. Use with place value charts for extra clarity.
- Decimal Numbers – Use to represent decimal numbers. One cube could represent one hundredth, one stick could represent one tenth and so on. This works well when used alongside place value charts.
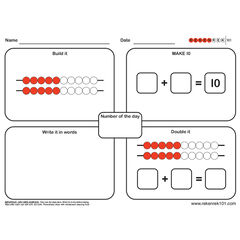
Rekenreks
Rekenreks are a popular and visual tool which are easy for children to use. They particularly help young children to group numbers. They also only require a small amount of desk space and no set up, making it an excellent ‘go-to’ resource in the classroom.
Here are some of the areas where you can use them:
- Counting – Can the children count in 1s, 2s, 5s, 10s? etc.
- Subitising up to 10 – Seeing a group of numbers in two different colours helps children to quickly recognise the number without counting. For example, 5 red beads and 2 white beads are quickly seen as 7 beads, rather than looking at 7 beads of all the same colour.
- Number Bonds – Move the beads to show number bonds to 10 and 20.
- Comparing Numbers – Move beads to explore numbers that are larger and smaller.
- Addition and Subtraction – Move the beads to physically add and subtract numbers within 20.
- Doubling and Halving – Move the beads to show the relationship between doubling and halving.
- Multiplication – Use to move beads into equal groups.
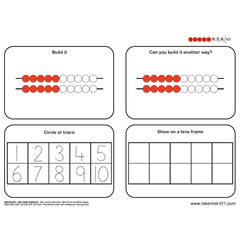
Ten Frames
Ten frames are an excellent resource for visually representing number and are incredibly versatile to use in the classroom.
Here are some of the areas where you can use them.
- Subitising – Place or draw counters in the frames. How many are there without counting? Use different coloured counters to make it easier to see the total number shown.
- Number bonds – Use different coloured counters in the frames to explore number bonds to 10 and 20.
- Addition – Use more than one frame to physically add the counters together on each frame. Children can also quickly see that a complete row on a tens frame is equal to 5 and a full frame of counters is equal to 10.
- Subtraction – Physically moving the counters off the frames help children to develop a solid understanding of amounts getting smaller after subtraction. Use more than one frame to create larger starting numbers.
- Represent Teen Numbers and Numbers Beyond 20 – Use a full frame of counters to show ten and that teen numbers are bigger than ten. Use two full frames to show 20 and numbers bigger than 20.
- Fractions – Show counters as representing a fraction and empty spaces as also representing a fraction, e.g. 6/10 filled and 4/10 empty.
Other Maths manipulatives that also offer great versatility and easily allow for delving deeper in a variety of Maths subject areas are:
Numicon, Counting Cubes, Number Rods, Dice, Dominoes and Bead Strings.
Top Tips for Using Maths Manipulatives
- Make them purposeful – Ensure that the manipulative used will clearly support the learning goals and will play a purposeful role in lessons.
- Introduce the Manipulative – Take time to introduce manipulatives to pupils and allow time for them to explore and play with the manipulatives, before using them more formally. Ask the children questions about how they would use them to help with maths.
- Model How to Use – After children have had time to freely explore the manipulatives, demonstrate how to use them to solve mathematical problems.
- Encourage Independence – Progress children from being told which manipulatives to use to solve a problem and how to use them, to them using them independently and confidently.
- Avoid Dependence – When children have developed a solid understanding of a concept using manipulatives and pictorial representations, move them away from visual representations onto being able to think in the abstract.
It is also important to remember that using manipulatives in conjunction with other manipulatives allows children to see a visual representation of a maths concept in more than one way. This is crucial for deepening understanding, developing logical reasoning and making connections when teaching for maths mastery.
For more advice on how to use manipulatives in maths teaching, see the NCETM website.
Using Maths Games and Activity Cards to Teach for Maths Mastery
Other useful resources for delving deeper into mathematical concepts and broadening children’s mathematical understanding are maths games and activity cards.
- Maths games provide an excellent opportunity to encourage collaborative learning and discussion.
- Activity cards are a fun way to develop children’s mathematical knowledge and depth of understanding. Children can also complete activities independently or in a pair or group. They decide themselves which calculations to use and whether to use manipulatives or pictorial representations to help them solve the problem.
Visit our Maths Mastery Resources page for a full range of resources to aid teaching for mastery.
Conclusion
Using concrete resources to teach maths mastery in a meaningful and purposeful way creates an engaging and interactive learning experience. These hands-on resources help to make mathematical concepts more real. This helps to bridge the gap between abstract ideas and concreate understanding. Most importantly, they help to raise confidence and reduce pupil anxiety, offering a fun approach to maths teaching. Overall, they provide the essential foundational building blocks for the mathematicians of tomorrow.
Written by Kelly Lawrence
Kelly has 15 years of experience working as a Primary School Teacher in both Key Stage 1 and 2.