Hi, my name is Dave Godfrey.  I’m a teacher and an independent primary mathematics consultant from York, and I’m passionate about the use of concrete resources.

The focus of this blog and its accompanying video is on the use of place value counters.

Place Value Counters and Base 10

Over 50 years ago, Zoltan Dienes proposed that children should have access to concrete materials and manipulatives to help them develop conceptual understanding of mathematical concepts.  His Base 10 materials help children develop deep understanding of place value and calculation. I’ve explored Base 10 in another of these videos.

In this video I’ve presented the number 1111 using both Base 10 and Place Value Counters. When I’ve been delivering training, I often ask teachers and teaching assistants which resource they prefer. Generally, the response is Base 10 because these blocks clearly show the cardinality of number – ten 1s are equivalent to one 10! Teachers also talk positively about the fact that place value counters have the value recorded on each disk, that they are smaller and cheaper!

I would suggest that there is a progression.Expose children to Base 10 first so they can grasp the cardinality of number and then provide the more abstract place value counters once that concept is in place.

Place Value Counters – Thousandths to Millions

A few years ago, the following calculation was in the Year 6 SAT paper: 122,456 – 11,999. A lot of children I met tried to solve this with the formal strategy. Two weeks after the test paper I remember working with a class of Year 6 children and exploring this calculation with them. I gave each child a place value grid and access to place value counters which spanned 100,000s through to 1s. We then modelled how simple this calculation was if you used a round and adjust strategy. We also modelled the ‘same difference’ or ‘manipulate the calculation’ strategy, where we increased both the minuend (122,456) and the subtrahend (11,999) by 1.  The equation became 122,457 – 12,000.

The place value counters provided a powerful tool for helping children understand these strategies. Each Tuesday I teach Year 6 in a local school here in York and I repeated the session. Because Base 10 only has 1, 10, 100 and 1000 pieces I couldn’t model this calculation with them. Place Value Counters made the learning possible.

By upper KS2 children are dealing with numbers up to millions and with thousandths. One of the great things about place value counters is that you can represent 9,345,923.312 with them!

Linking Base 10 imagery, Place Value Counters and Story

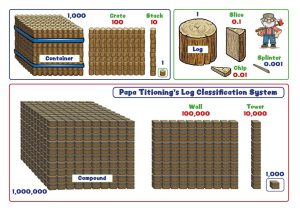
Zoltan Dienes was not just a big fan of using concrete resources, but he was also a proponent of one of my passions – using story in learning. Papa Titioning is one of my Number Fun characters.  He is a lumberjack and organises his logs to represent our Base 10 number system. The imagery mirrors our Base 10 equipment and extends the use of the log analogy from thousandths through to millions.  In the video I include the imagery of Papa Titioning’s Log Classification System. Now, when children are using Place Value Counters to explore place value or calculation, they have a story context to support their understanding.  I’ll return to this in a moment.

Types of Place Value Counters

There are many types of Place Value Counters on the market. There are big foam versions available and also different sets made from foam or plastic. Some have values on both sides and some only on one side. While, some have alternative fraction and decimal notation of either side for 0.1s and 0.01s. Some are 19mm in diameter and some 2.5cm.  It’s worth having a look around for the counters that best suit your needs.

Place Value Counters and Place Value Grids – Tools for Place Value & Calculation

Place Value Counters work well with place value grids. As I model in the video, I train children to place the counters carefully within a grid to show a 10’s frame layout, i.e., 7 counters would be arranged in a 5 and a bit configuration. The video concludes with a demonstration of how I use place value counters, a place value grid and Papa Titioning’s Division Song video to help children grasp conceptual understanding of short division.

Place Value Counters and Tens Frames

Place Value Counters work well with tens frames too.  Here I model how they might be used in paper tens frames, plastic frames and egg box tens frames.  The very arrangement of putting Place Value Counters into tens frames helps children understand the concepts of exchanging and regrouping numbers.

PVC and Part Whole Model

I also spend a few moments modelling how place value counters are a great tool for modelling both standard and non-standard partitioning within a part-whole model that have two, three and four-parts.

 Your use of Place Value Counters in school

Place Value Counters are powerful tools that fit perfectly with the CPA (Concrete, Pictorial and Abstract) approach within the teaching of mathematical mastery. The fact that Place Value Counters give us a manipulative for place value and calculation that spans number from hundredths through to millions is brilliant.  I’d encourage you to add Papa Titioning’s Log Classification System to provide both pictorial representations and story to underpin their understanding.

This video may act as a bit of an introduction, but I’m sure there are a host of ideas that I haven’t covered.

How effective are you finding the use of place value counters in your school?

Please do share how you’re creatively using place value counters with your children – I’d love to know!